Frequency partition of a graph
In graph theory, a discipline within mathematics, the frequency partition of a graph (simple graph) is a partition of its vertices grouped by their degree.For example, the degree sequence of the left-hand graph below is (3, 3, 3, 2, 2, 1) and its frequency partition is 6 = 3 + 2 + 1. This indicates that it has 3 vertices with some degree, 2 vertices with some other degree, and 1 vertex with a third degree. The degree sequence of the bipartite graph in the middle below is (3, 2, 2, 2, 2, 2, 1, 1, 1) and its frequency partition is 9 = 5 + 3 + 1. The degree sequence of the right-hand graph below is (3, 3, 3, 3, 3, 3, 2) and its frequency partition is 7 = 6 + 1.
In general, there are many non-isomorphic graphs with a given frequency partition. A graph and its complement have the same frequency partition. For any partition p = f1 + f2 + ... + fk of an integer p > 1, other than p = 1 + 1 + 1 + ... + 1, there is at least one (connected) simple graph having this partition as its frequency partition.[1]
Frequency partitions of various graph families are completely identifieds; frequency partitions of many families of graphs are not identified.
Contents |
Frequency partitions of Eulerian graphs
For a frequency partition p = f1 + f2 + ... + fk of an integer p > 1, its graphic degree sequence is denoted as ((d1)f1,(d2)f2, (d3)f3, ..., (dk) fk) where degrees di's are different and fi ≥ fj for i < j. Bhat-Nayak et al. (1979) showed that a partition of p with k parts, k ≤ integral part of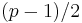 
is a frequency partition[2] of a Eulerian graph and conversely. The graphic degree sequences of the partitions are:
- For p =
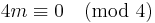, ...(2m + 2)f3,(2m)f1,(2m − 2)f2, ... , example, for 12 = 5 + 4 + 3, the Eulerian degree sequence is 83,65,44.
- For p =
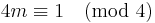, ...(2m + 2)f2,(2m)f1,(2m − 2)f3, ... , example, for 13 = 6 + 4 + 3, the Eulerian degree sequence is 84,66,43.
- For p =
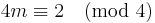, ...(2m + 2)f2,(2m)f1,(2m − 2)f3, ... , example, for 14 = 6 + 5 + 3, the Eulerian degree sequence is 85,66,43.
- For p =
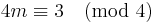, ...(2m + 4)f3,(2m + 2)f1,(2m)f2, ... , example, for 15 = 6 + 5 + 4, the Eulerian degree sequence is 104,86,65.
Frequency partition of trees, Hamiltonian graphs, tournaments and hypegraphs
The frequency partitions of families of graphs such as trees,[3] Hamiltonian graphs[4] directed graphs and tournaments[5] and to k-uniform hypergraphs.[6] have been characterized.
Unsolved problems in frequency partitions
The frequency partitions of the following families of graphs have not yet been characterized:
References
- ^ Chinn, P. Z. (1971), "The frequency partition of a graph. Recent Trends in Graph Theory", Lecture Notes in Mathematics (Berlin: Springer-Verlag) 186: pp. 69–70
- ^ Bhat-Nayak, Vasanti N.; Naik, Ranjan N. & Rao, S. B. (1979), Characterization of Frequency Partitions of Eulerian Graphs, in Rao, A. R., "ISI Lecture Notes", Proc. Symposium on graph Theory (The MacMillan comp. of India) 4. Also in Lecture Notes in Mathematics, Combinatorics and Graph Theory, Springer-Verlag, New York, Vol. 885 (1980), p 500.
- ^ Rao, T. M. (1974), "Frequency sequences in Graphs", Journal of Combinatorial Theory B 17: 19–21
- ^ *Bhat-Nayak, Vasanti N.; Naik, Ranjan N. & Rao, S. B. (1977), "Frequency partitions: forcibly pancyclic and forcibly nonhamiltonian degree sequences", Discrete Mathematics 20: 93–102
- ^ Alspach, B. & Reid, K. B. (1978), "Degree Frequencies in Digraphs and Tournaments", Journal of Graph Theory 2: 241–249, doi:10.1002/jgt.3190020307
- ^ Bhat-Nayak, V. N. & Naik, R. N. (1985), "Frequency partitions of k-uniform hypergraphs", Utilitas Math. 28: 99–104
- ^ S. B. Rao, A survey of the theory of potentially p-graphic and forcibly p-graphic sequences, in: S. B. Rao edited., Combinatorics and Graph Theory Lecture Notes in Math., Vol. 885 (Springer, Berlin, 1981), 417-440